DC machine permanent magnet model
Model assumptions
Configuration of the machine electrical system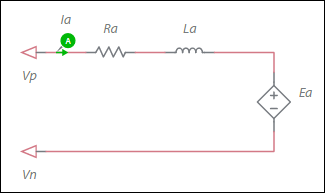
Ea = ωm * Ke
where
Ea = back-EMF voltage
ωm = Mechanical angular speed
Ke = Torque constant
The generated electromagnetic torque is:
Te = Ia * Kt
where
Kt = Torque constant
| Parameter | Description |
|---|---|
| Armature inductance | Inductance of the armature winding. |
| Armature resistance | Ra in the equation in Deriving Ke, Kt and Ra from Datasheets, below. |
| Speed constant | Speed constant in V•s/rad. This is usually defined on datasheets (Ke). If not, refer to Deriving Ke, Kt and Ra from Datasheets, below. |
| Torque constant | If it is not specified on the datasheet, it is in most cases adequate to set it to the same value as Ke. See also, Deriving Ke, Kt and Ra from datasheets, below. |
| Shaft inertia | Inertia of the shaft in kg*m<sup>2</sup>. J<sub>rotor</sub> on the machine model diagram in <a href="/help/components/machine-modeling/">Machine modeling</a>. |
| Shaft friction | This is F<sub>rotor</sub> on the machine model diagram in <a href="/help/components/machine-modeling/">Machine modeling</a>. |
| Initial angular speed | Rotational measurement of the shaft angle in rad/s at the start of the simulation. |
| Initial angle | Initial shaft angle in radians. |
Deriving Ke, Kt and Ra from datasheets
Some datasheets may not explicitly state the static parameters Ke, Kt, and Ra but these parameters may easily be derived from stated data.
The static torque-speed curve for a linear DC machine, as represented by this model, is a downward sloping line, described by the following equation:
![]()
where
Vt = terminal voltage applied to the machine
ωm = speed in rad/s
T = generated torque in Nm
Ra = armature resistance
Ke and Kt are the speed and torque constants which are usually equal in value.
Datasheets often provide operating points such as no-load speed, stall torque, and rated speed/torque conditions, all of which, by definition, lie on the torque-speed curve. Therefore it is a matter of solving for the unknowns in the torque-speed equation.
Using the no-load speed, ωo, Ke may be calculated as:
![]()
